Rabu, 31 Oktober 2018

FAKTA-FAKTA LOUIS TOMLINSON! NO.7 MENCENGANGKAN

By Lelaki IdamanOktober 31, 2018Kimia Tidak ada komentar:

Cara Mudah Menggam

bar Struktur Lewis Suatu Molekul

Judul tulisan ini adalah cara mudah menggambarkan struktur Lewis suatu molekul, meskipun cara termudahnya hanyalah dengan banyak berlatih dengan mengikuti urutan yang disarankan seperti yang ada pada tulisan ini. Dengan langkah-langkah seperti yang tertulis tentu akan menjadi lebih mudah menggambarkan struktur Lewis suatu molekul.

Struktur Lewis dari suatu molekul adalah cara menggambarkan bagaimana atom-atom berikatan membentuk molekul dengan menggunakan penanda seperti noktah atau tanda x untuk mewakili elektron yang terlibat dalam pembentukan molekul. Elektron yang terlibat ini biasanya hanya elektron valensi (elektron yang berada di kulit terluar).

Untuk penjelasan lebih joss dan lebih mudah dan update terbaru tentang Struktur Lewis, Hibridisasi, Bentuk Molekul, dan lain-lain silakan klik pranala ini.
Prinsip dalam menggambarkan struktur Lewis suatu molekul adalah mengupayakan agar elektron di sekitar atom dalam setiap molekul berjumlah delapan atau mengikuti aturan oktet. Dengan memiliki elektron sebanyak 8 setiap atom diharapkan menjadi stabil dengan membentuk ikatan.
Untuk itu sebelum dapat menggambar struktur Lewis suatu molekul harus memahami bagaimana menentukan konfigurasi elektron setiap atom. Biasanya dalam soal-soal disertai dengan data nomor atom setiap unsur yang akan digunakan, tujuannya tidak lain agar dapat menuliskan konfigurasi elektronnya sehingga elektron valensinya juga dapat diketahui.
CARA MENGGAMBAR STRUKTUR LEWIS UNTUK MOLEKUL YANG TIDAK MENGANDUNG ATOM BERMUATAN

Hitung jumlah semua elektron valensi untuk setiap atom dalam molekul (selanjutnya dalam tulisan ini disebut total elektron valensi).
Hitung jumlah elektron valensi setiap atom dalam molekul jika atom-atom itu sesuai aturan oktet (selanjutnya dalam tulisan ini disebut total elektron oktet). Aturan oktet menyatakan bahwa semua atom harus memiliki delapan elektron valensi (kecuali untuk hidrogen, yang cukup dua saja, dan boron dengan enam elektron).
Hitung selisih jumlah elektron yang sesuai aturan oktet dengan jumlah elektron valensi nyatanya (hasil pada langkah #2 dikurangi hasil pada langkah #1). Selisih ini akan sama dengan jumlah elektron yang digunakan berikatan dalam molekul. (selanjutnya dalam tulisan ini disebut total elektron berikatan)
Bagilah jumlah elektron berikatan dengan angka dua: Ingat, karena setiap ikatan memiliki dua elektron, jumlah elektron yang digunakan bersama dua atom yang berikatan. Hasil bagi ini merupakan jumlah ikatan yang akan digunakan dalam molekul. (selanjutnya dalam tulisan ini disebut jumlah ikatan)
Gambarkan susunan atom untuk molekul dengan jumlah ikatan yang diperoleh pada langkah #4 di atas: Beberapa aturan berguna untuk diingat adalah ini:

- Hidrogen dan halogen: berikatan sekali.
- Golongan oksigen: berikatan dua kali.
- Golongan nitrogen: berikatan tiga kali. Begitu pula boron.
- Golongan karbon: berikatan empat kali.

Sebaiknya ikatan-ikatan yang dipasang antaratom adalah ikatan tunggal terlebih dahulu, dan kemudian menambahkan beberapa ikatan (jika diperlukan) sampai aturan diatas diikuti.

Catatan: Unsur yang lebih elektroprositif atau kurang elektronegatif (dalam tabel periodik unsur letaknya di sebelah kiri (kecuali H) atau sebelah bawah atau jari-jari atomnya lebih besar) lebih mungkin sebagai atom pusat. Perkecualian pada Cl₂O, O yang berperan sebagai atom pusat. H tidak akan pernah sebagai atom pusat. Atom pusat ketika membentuk ikatan harus mengikuti aturan oktet, kecuali Be hanya 4 elektron ikatan dan B hanya 6 elektron ikatan.

Tentukan jumlah pasangan elektron bebas (tak berikatan). Caranya hitung jumlah elektron valensi – jumlah elektron yang digunakan untuk berikatan

atau dengan cara kurangi hasil hitung langkah #1 dengan hasil hitung pada langkah # 3.

Tata semuanya di sekitar atom sampai semua memenuhi aturan oktet: Ingat, SEMUA unsur agar di sekitarnya ada delapan elektron, secara total (KECUALI hidrogen). Hidrogen cukup dua elektron. Oh ya untuk unsur yang terletak pada periode 3 (misalnya S belerang) sering jumlah elektron disekitarnya lebih dari delapan, dengan pertimbangan muatan formalnya nol akan lebih disukai.

Menguji keberadaan muatan formal, (muatan formal ini adalah muatan semu, hasil perbandingan antara elektron valensi setiap atom dengan jumlah elektron yang dimiliki ketika membentuk ikatan dengan atom yang lain).

Muatan formal tiap atom = elektron valensi atom – jumlah ikatan dengan atom lain – jumlah elektron bebas (tidak digunakan berikatan) yg dimiliki.

Contoh penerapan untuk molekul CH₂O

Total elektron valensi adalah 12.

2 elektron valensi H (2 atom H × 1 elektron/atom = 2 elektron)
4 elektron valensi C (1 atom C × 4 elektron/atom) = 4 elektron)
6 elektron valensi O (1 atom O × 6 elektron/atom) = 6 elektron)
Jumlah elektron valensi pada CH₂O = 2+4+6 = 12 elektron

Total elektron oktet semua atom dalam CH₂O = 20, diperoleh dari:

(2 atom H × 2 elektron) + 1atom C × 8 elektron) + (1 atom O × 8 elektron) = 4 + 8 + 8 = 20 elektron.

Total elektron berikatan sama dengan total elektron oktet dikurangi total elektron valensi, atau 20 – 12 = 8.

Jumlah ikatan = total elektron berikatan dibagi dua, karena ada dua elektron per ikatan. Akibatnya, di CH₂O, jumlah ikatannya = 4. (Karena 8/2 adalah 4).

Penggambaran struktur Lewis, tuliskan atom C di tengah dan atom lainnya (2 atom H dan 1 atom O) berada di sekeliling atom C. Cantumkan elektron berikatan (masing-masing 2 elektron setiap ikatan) di antara atom pusat (C) dengan atom yang ada disekitarnya, antara atom C dan O yang paling mungkin memiliki ikatan rangkap 2 (double bond). Lakukan hingga semua (dalam hal ini 8 elektron berikatan terpakai).
Jumlah pasangan elektron bebas = total elektron valensi (dari # 1) dikurangi total elektron berikatan (dari # 3), yang dalam contoh ini sama dengan 12 – 8, atau 4. Melihat struktur CH₂O, dapat dilihat bahwa karbon sudah memiliki delapan elektron di sekitarnya. Oksigen, hanya memiliki empat elektron di sekitarnya (lihat gambar pada nomor 5 di atas). Untuk melengkapi gambar, masing-masing oksigen harus memiliki dua set pasangan elektron bebas, Tambahkan pasangan elektron bebas pada atom O sehingga aturan oktet terpenuhi.seperti dalam struktur Lewis berikut:

Menguji ada tidaknya muatan formal tiap atom.

Muatan formal C = 4 (e.valensi) – 4 (jumlah ikatan) – 0 (jumlah elektron bebas) = 0

Muatan formal H = 1 – 1 – 0 = 0

Muatan formal O = 6 – 2 – 4 = 0

Jadi benar bahwa molekul CH₂O ini tidak bermuatan alias netral.

Contoh penerapan untuk molekul H₂CO₃

Total elektron valensi adalah 24.

2 elektron valensi H (2 atom H × 1 elektron/atom = 2 elektron)
4 elektron valensi C (1 atom C × 4 elektron/atom) = 4 elektron)
18 elektron valensi O (3 atom O × 6 elektron/atom) = 18 elektron)
Total elektron valensi pada H₂CO₃ = 24 elektron

Total elektron oktet semua atom dalam H₂CO₃ = 36, diperoleh dari:

(2 atom H × 2 elektron) + 1atom C × 8 elektron) + (3 atom O × 8 elektron) = 4 + 8 + 24 = 36 elektron.

Total elektron berikatan sama dengan total elektron oktet dikurangi total elektron valensi, atau 36 – 24 = 12.

Jumlah ikatan = total elektron berikatan dibagi dua, karena ada dua elektron per ikatan. Akibatnya, di H₂CO₃, jumlah ikatannya = 6. (Karena 12/2 adalah 6).

Penggambaran struktur Lewis, tuliskan atom C di tengah dan atom lainnya (2 atom H dan 3 atom O) berada di sekeliling atom C. Cantumkan elektron berikatan (masing-masing 2 elektron setiap ikatan) di antara atom pusat (C) dengan atom yang ada disekitarnya, perhatikan antara atom C dan O ada yang memungkinkan memiliki ikatan rangkap 2 (ikatan dobel). Lakukan hingga semua elektron berikatan terpakai (dalam hal ini 12 elektron berikatan terpakai atau dengan sistem garis, 6 garis).

Jumlah pasangan elektron bebas = total elektron valensi (dari # 1) dikurangi total elektron berikatan (dari # 3), yang dalam contoh ini sama dengan 24 – 12, atau 12. Melihat struktur H₂CO₃, dapat dilihat bahwa karbon sudah memiliki delapan elektron (empat ikatan) di sekitarnya. Setiap oksigen akan mendapat bagian masing-masing 2 pasang elektron bebas untuk memenuhi aturan oktet, untuk atom H sudah memenuhi aturan duplet. H₂CO₃ mempunyai struktur Lewis:

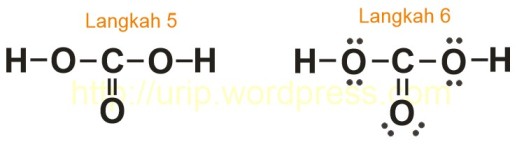
Menguji ada tidaknya muatan formal tiap atom.

Muatan formal C = 4 (e.valensi) – 4 (jumlah ikatan) – 0 (jumlah elektron bebas) = 0
Muatan formal H = 1 – 1 – 0 = 0 —–pada moleluk ini kedua atom H muatan formalnya sama.
Muatan formal O (yang berikatan rangkap dengan C) = 6 – 2 – 4 = 0
Muatan formal O (yang berikatan dengan C dan H) = 6 – 2 – 4 = 0

Jadi benar bahwa molekul H₂CO₃ ini tidak bermuatan alias netral.
CARA MENGGAMBAR STRUKTUR LEWIS UNTUK MOLEKUL YANG MENGANDUNG SATU ATAU LEBIH ATOM BERMUATAN
Cara ini pada dasarnya adalah sama dengan cara di atas, kecuali ada beberapa aturan tambahan. Perubahan prosedur di atas diuraikan dengan huruf berwarna merah.

Hitung jumlah semua elektron valensi untuk setiap atom dalam molekul (selanjutnya dalam tulisan ini disebut total elektron valensi). Untuk anion poliatomik, tambahkan muatan ion (jumlah elektron yang diterima) dengan jumlah elektron valensi.. Untuk kation poliatomik, kurangi muatan ion (jumlah elektron yang dilepas) dari jumlah elektron valensi.
Hitung jumlah elektron valensi setiap atom dalam molekul jika atom-atom itu sesuai aturan oktet (selanjutnya dalam tulisan ini disebut total elektron oktet). Aturan oktet menyatakan bahwa semua atom harus memiliki delapan elektron valensi (kecuali untuk hidrogen, yang cukup dua saja, dan boron dengan enam elektron).
Hitung selisih jumlah elektron yang sesuai aturan oktet dengan jumlah elektron valensi nyatanya (hasil pada langkah #2 dikurangi hasil pada langkah #1). Selisih ini akan sama dengan jumlah elektron yang digunakan berikatan dalam molekul (selanjutnya dalam tulisan ini disebut total elektron berikatan).
Bagilah jumlah elektron berikatan dengan angka dua: Ingat, karena setiap ikatan memiliki dua elektron, jumlah elektron yang digunakan bersama dua atom yang berikatan. Hasil bagi ini merupakan jumlah ikatan yang akan digunakan dalam molekul (selanjutnya dalam tulisan ini disebut jumlah ikatan).
Gambarkan susunan atom untuk molekul dengan jumlah ikatan yang diperoleh pada langkah #4 di atas: Beberapa aturan berguna untuk diingat adalah ini:

- Hidrogen dan halogen: dapat berikatan sekali.
- Golongan Oksigen dapat berikatan satu, dua, atau tiga kali.
- Golongan Nitrogen dapat berikatan dua, tiga, atau empat kali
- Golongan Boron biasanya dapat berikatan empat kali.
- Golongan Karbon dapat berikatan empat kali.

Sebaiknya ikatan-ikatan yang dipasang antaratom adalah ikatan tunggal terlebih dahulu, dan kemudian menambahkan beberapa ikatan (jika diperlukan) sampai aturan diatas diikuti. Catatan unsur yang lebih elektroprositif atau kurang elektronegatif (dalam tabel periodik unsur letaknya di sebelah kiri (kecuali H) atau sebelah bawah atau jari-jari atomnya lebih besar) lebih mungkin sebagai atom pusat.

Tentukan jumlah pasangan elektron bebas (tak berikatan). Caranya hitung jumlah elektron valensi – jumlah elektron yang digunakan untuk berikatan

atau dengan cara kurangi hasil hitung langkah #1 dengan hasil hitung pada langkah # 3.

Tata semuanya di sekitar atom sampai semua memenuhi aturan oktet: Ingat, SEMUA unsur agar di sekitarnya ada delapan elektron, secara total (KECUALI hidrogen). Hidrogen cukup dua elektron. Catatan unsur yang dalam tabel periodik unsur letaknya di sebelah kiri (kecuali H) lebih mungkin sebagai atom pusat.

Untuk menentukan apakah atom memiliki muatan, bandingkan jumlah elektron setiap atom dengan jumlah elektron valensi normalnya. Langkah ini sama dengan kita menguji keberadaan muatan formal setiap atom dalam molekul, sehingga pada bagian akhir kita akan tahu molekul itu bermuatan atau tidak, kalau bermuatan kita jadi tahu atom mana yang menyumbang muatan tersebut.

Untuk tujuan ini (tinjauan tiap atom), setiap ikatan dihitung hanya satu elektron dan setiap pasangan elektron bebas dihitung dua elektron.

Jika jumlah elektron yang dimiliki atom lebih dari jumlah elektron valensi normal, maka atom memiliki muatan negatif. Jika jumlahnya kurang dari jumlah elektron valensi normal, maka atom bermuatan positif. Jika itu sama dengan keadaan normal, maka atom tidak bermuatan.

Contoh penerapan untuk molekul CO₃^2-

Total elektron valensi adalah 24.

4 elektron valensi C (1 atom C × 4 elektron/atom) = 4 elektron)
18 elektron valensi O (3 atom O × 6 elektron/atom) = 18 elektron)
2 elektron yang diterima (karena ion bermuatan 2-)
Jumlah elektron valensi pada CO₃^2- dianggap = 24 elektron

Total elektron oktet semua atom dalam CO₃^2- = 32, diperoleh dari:

(1 atom C × 8 elektron) + (3 atom O × 8 elektron) = 8 + 24 = 32 elektron.

Total elektron berikatan = total elektron oktet dikurangi total elektron valensi, atau 32 – 24 = 8.

Jumlah ikatan = total elektron berikatan dibagi dua, karena ada dua elektron per ikatan. Akibatnya, di CO₃^2-, jumlah ikatannya = 4. (Karena 8/2 adalah 4).

Penggambaran struktur Lewis, tuliskan atom C di tengah dan 3 atom O berada di sekeliling atom C. Cantumkan elektron berikatan (masing-masing 2 elektron setiap ikatan atau langsung dengan menuliskan garis ikatan (perikatan 2 elektron)) di antara atom pusat (C) dengan atom O yang ada disekitarnya, perhatikan antara atom C dan O ada yang memungkinkan memiliki ikatan rangkap 2 (ikatan dobel). Lakukan hingga semua elektron berikatan terpakai (dalam hal ini 8 elektron berikatan terpakai atau dengan sistem garis, 4 garis).

Jumlah pasangan elektron bebas = total elektron valensi (dari # 1) dikurangi total elektron berikatan (dari # 3), yang dalam contoh ini sama dengan 24 – 8, atau 16. Melihat struktur CO₃^2-, dapat dilihat bahwa karbon sudah memiliki delapan elektron (4 ikatan) di sekitarnya. Pada O yang berikatan rangkap dengan C hanya perlu 2 pasangan elektron bebas hingga memenuhi aturan oktet, dua O lainnya masing-masing perlu 3 pasang elektron bebas untuk memenuhi aturan oktet karena antara O dan C hanya berikatan tunggal (yang sama dengan punya dua elektron)
Menentukan atom manakah yang kemungkinan bermuatan adalah dengan membandingkan elektron yang dimiliki dengan elektron valensi normalnya. Dalam hal ini O yang ada di kiri dan kanan atom C elektronnya berlebih satu dari jumlah elektron valensi yang seharusnya. Seharusnya hanya punya 6 tetapi pada bagian tersebut O punya 7 elektron (6 + 1 elektron diambil dari elektron ikatan antara dirinya dengan atom C).

Tulisan ini diadaptasi dari http://misterguch.brinkster.net/lewisstructures.html dan http://chemistry.umeche.maine.edu/CHY251/therules.html
Video-video tentang penjelasan struktur lewis dapat ditonton atau diunduh dari sini. Pada link tersebut terdapat lebih dari 70 struktur Lewis.
Pranala lain untuk video cara menggambar struktur Lewis ada di web thegeoexchange.org.
Selamat belajar dan wassalam.

MATEMATIKA WAJIB? BAWA SUSAH AJA

By Lelaki IdamanOktober 31, 2018Matematika Wajib Tidak ada komentar:

Materi Persamaan dan Pertidaksamaan Linier Kelas 10

Materi Persamaan dan Pertidaksamaan Linier Kelas 10 - Materi Persamaan dan Pertidaksamaan Linier ini adalah bab 2 dari pelajaran matematika kelas 10.

Persamaan linear

Persamaan linear adalah persamaan yang pangkat variabelnya adalah satu. Bentuk umum persamaan linear adalah ax + b = c, a ≠ 0, a,b,c E R

Menyelesaikan persamaan linear adalah mencari pengganti variabel sehingga persamaan menjadi pernyataan yang bernilai benar

Contoh 1

Selesaikan 3x + 4 =16 !

Jawab

Agar 3x + 4 = 16 maka x diganti dengan 4, jadi penyelesaiannya x = 4

Sifat-sifat persamaan linear:

suatu persamaan tidak berubah nilainya jika ditambah atau dikurang dengan bilangan yang sama.

Suatu persamaan tidak berubah nilainya jika kedua ruas dikalikan atau dibagi dengan bilangan yang sama.

Contoh:

Tentukan penyelesaian dari persamaan:

6x –18 = 0

Jawab:

6x – 18 = 0

6x – 18 + 18 = 0 + 18 (kedua ruas ditambah 18)

6x = 18

(kedua ruas dibagi 6 supaya ruas kiri hanya ada x)

x = 3

(Kedua ruas dikurangi 6)

(kedua ruas dikurangi 2x)

Jadi penyelesaiannya 12

Untuk memperpendek langkah-langkah penyelesaian maka ada langkah-langkah yang tidak perlu ditulis.

Contoh:

Untuk contoh soal a langkah-langkahnya menjadi :

6x – 18 = 0

6x =18

Untuk contoh soal b langkah – langkahnya menjadi:

2. Pertidaksamaan Linier

Pertidaksamaan adalah kalimat terbuka yang menggunakan tanda <, > , ≤ , ≥

Contoh:

5 + x >10

x – 4 < 12

3x – 2 ≤ 7

2x + 6 ≥ 4

Ketidaksamaan adalah kalimat tertutup yang menggunakan tanda <, >, ≤, ≥

contoh:

7 + 3 ≥ 15

2 -6 < -4 + 10

3 x 5 ≤ 5 x 6

20 : 2 > 9 : 4

Penyelesaian Pertidaksamaan adalah konstanta pengganti variabel yang menyebabkan suatu pertidaksamaan menjadi kalimat yang benar.

Himpunan penyelesaian pertidaksamaan adalah himpunan yang memuat semua penyelesaian Pertidaksamaan linier.

Sifat-sifat pertidaksamaan :

Suatu pertidaksamaan tidak berubah tandanya jika kedua ruas pertidaksamaan ditambah atau dikurangi dengan bilangan yang sama misal x > y maka x + a > y + a

Suatu pertidaksamaan tidak berubah tandanya jika kedua ruas dikali atau dibagi dengan bilangan positif yang sama, misalnya x ≤ y maka a .x ≤ y. a dengan a > 0

Suatu pertidaksamaan akan berubah tandanya jika kedua ruas dikali atau dibagi dengan bilangan negatif yang sama misal x ≤ y maka –x a ≥ -y a (berubah tanda karena kedua ruas dikali dengan bilangan negatif yang sama) misal x ≤ y maka

(berubah tanda karena kedua ruas dibagi dengan bilangan negatif yang sama.)

Penyelesaian pertidaksamaan

Materi himpunan penyelesaian dari suatu pertidaksamaan dapat ditunjukan dendan notasi himpunan atau dengan garis bilangan.

Jika HP ditunjukan dengan garis bilangan , maka tanda < atau ≤ digambarkan dengan anak panah ke kiri, sedangkan tanda > atau ≥ digambarkan dengan anak panah ke kanan.

Titik yang menyatakan bilangan tertentu , maka tanda < atau > digambarkan dengan tanda kurung biasa, sedangkan tanda ≤ atau ≥ digambarkan dengan tanda kurung siku

Contoh 1

Tentukan HP dan gambar pada garis bilangan dari pertidaksamaan

3(x – 1) + 1 < 7

Jawab:

3( x – 1) + 1 < 7

3 x –3 + 1 < 7 Ruas kiri diselesaikan terlebih dahulu

3 x –2 < 7

3x –2 + 2 < 7 + 2 Kedua ruas ditambah lawan dari –2 yaitu 2

3 x < 9

Kedua ruas dikali dengan kebalikan dari 3 yaitu

HP = { x | x < 3 , x

Contoh 2

Tentukan HP dan gambar grafik garis bilangan dari suatu pertidaksamaan

–2 ≤ 2 x – 4 ≤ 2 + x

Jawab:

Pertidaksamaan –2 ≤ 2 x – 4 ≤ 2 + x terdapat dua tanda pertidaksamaan maka ada tiga ruas (ruas kiri, ruas tengah, ruas kanan) sehingga ada dua penyelesaian. Penyelesaian pertama , bentuk pertidaksamaannya adalah

- 2 ≤ 2 x – 4 Ruas kiri dan ruas tengah …….(a)

-2 x ≤ -4 +2

-2 x ≤ -2

x ≥ 1 Berubah tandanya karena kedua ruas dibagi dengan –2

HP= {x | x ≥ 1, x

Penyelesaian kedua , bentuk pertidaksamaannya adalah

2 x – 4 ≤ 2 + x Ruas tengah dan ruas kiri …..(b)

2 x – x ≤ 2 + 4

x ≤ 6

HP 6 HP = {x | x ≤ 6, x

Pertidaksamaan –2 ≤ 2 x – 4 ≤ 2 + x terdapat dua nilai x yaitu x ≥1 dan x ≤ 6 atau 1 ≤ x ≤ 6

Jika kedua grafik bilangan tersebut diatas digabung maka

Penyelesaian (a)

Penyelesaian (b)

Gabungan

Sehingga HP = {x | 1 ≤ x ≤ 6 , x

Logaritma Lewat Ajaaaa~~~~

By Lelaki IdamanOktober 31, 2018Matematika Minat Tidak ada komentar:

Fungsi Eksponen dan Logaritma

A. Fungsi Eksponen
Fungsi adalah relasi yang bersifat khusus.
Ada dua bentuk umum fungsi eksponen, yaitu
a. Fungsi eksponen dengan bilangan basis $a>1$
Perhatikan ilustrasi berikut

[Sumber]

Perhatikan juga tabel berikut

$\begin{tabular}{|r|l|c|r|c|c|}\hline x&-2&-1&0&1&2\\ \hline f(x)&{1/4}&{1/2}&1&2&4\\ \hline (x,f(x))&(-2,1/4)&(-1,1/2)&(0,1)&(1,2)&(1,4)\\ \hline\end{tabular}$

b. Fungsi eksponen dengan bilangan basis $0<a<1$
Perhatikan pula ilustrasi berikut ini

[Sumber]

Perhatikan pula tabel berikut

$\begin{tabular}{|r|l|c|r|c|c|}\hline x&-2&-1&0&1&2\\ \hline f(x)&{4}&{2}&1&1/2&1/4\\ \hline (x,f(x))&(-2,4)&(-1,2)&(0,1)&(1,1/2)&(1,1/4)\\ \hline\end{tabular}$

Sifat-sifat pada bilangan bentuk eksponen

[Sumber]
Silahkan anda pelajari beberapa bentuk persamaan eksponen dan langkah penyelesaiannya.
Sebagai tambahan $a^{a^{a+m}}=a^{a^{a+n}}\: \Rightarrow \: \: m=n$ .
$\LARGE\fbox{Contoh Soal}$ 1. Tentukan penyelesaian dari $\sqrt{8^{x-1}}=2.\sqrt[3]{\left ( \frac{1}{4} \right )}$
Jawab:
$8^{\frac{x-1}{2}}=2.2^{-\frac{2}{3}}\: \Rightarrow\: 2^{\frac{3(x-1)}{2}}=2^{\frac{1}{3}}$ $\frac{3x-3}{2}=\frac{1}{3}\: \Rightarrow \: 3x-3=\frac{2}{3}\: \Rightarrow \: x=\frac{11}{9}$ Ingat: $a^{f(x)}=a^{p}\: \Rightarrow \: f(x)=p\: ,\: dengan\: syarat\: (a>0\: ,\: a\neq 1)$
2. Tentukanlah penyelesaian dari $5^{x^{2}+3x+5}=\left ( \frac{1}{5} \right )^{2x+1}$
Jawab:
$5^{x^{2}+3x+5}=5^{-2x-1}$ $x^{2}+3x+5=-2x-1\: \Rightarrow \: x^{2}+5x+6=0$ $\left ( x+3 \right )\left ( x+2 \right )=0\: \Rightarrow \: x_{1}=-3\: \: atau\: \: x_{2}=-2$ Ingat: $a^{f(x)}=a^{g(x)}\: \Rightarrow \: f(x)=g(x)\: ,\: dengan \: syarat\: (a>0\: dan\: a\neq 1)$
3. Tentukan penyelesaian dari $5^{x^{2}-3x+2}=3^{x^{2}-3x+2}$
Jawab:
Penyelesaiannya adalah $x^{2}-3x+2=0\: \Rightarrow \: \left ( x-1 \right )\left ( x-2 \right )=0\: \Rightarrow \: x_{1}=1\: \: atau\: \: x_{2}=2$
Ingat: $a^{f(x)}=b^{f(x)}\: \Rightarrow \: f(x)=0$
4. Tentukan penyelesaian dari $7^{3x-1}=5^{2x+1}$
Jawab:
$7^{3x-1}=5^{2x+1}$ , kemudian dilogkan keduanya, sehingga
$\log 7^{3x-1}=\log 5^{2x+1}$ $(3x-1)\log 7=(2x+1)\log 5$ ,
$3x\log 7-2x\log 5=\log 5+\log 7$ ,
$x\left ( \log 7^{3}-\log 5^{2} \right )=\log 35\: \Leftrightarrow \: x\log \left ( \frac{343}{25} \right )=\log 35$ ,
$x=\left ( \frac{\log 35}{\log \left ( \frac{343}{25} \right )} \right )$ ,
$Jadi,\: \: x=^{\frac{343}{25}}\log 35$
5. Tentukan semua solusi dari persamaan eksponen $(x-3)^{x^{2}+3x-2}=x^{2}-6x+9$
Jawab:
$(x-3)^{x^{2}+3x-2}=x^{2}-6x+9\: \Leftrightarrow \: (x-3)^{x^{2}+3x-2}=(x-3)^{2}$
Untuk bentuk $f(x)^{g(x)}=f(x)^{h(x)}$
ada 4 syarat yang perlu diperhatikan, antara lain:

Pertama: $eksponen \: sama \: \: atau\: \: g(x)=h(x)$
Kedua: Bilangan basis $f(x)=0$ , dengan ketentuan baik $g(x)\: dan\: h(x)$ keduanya positif, atau $g(a)\times h(a)=positif$
Ketiga: Bilangan basis $f(x)=1$
Keempat: Bilangan basis $f(x)=-1$ , dengan syarat $g(a)+h(a)=genap$

Sehingga
Pertama: $x^{2}+3x-2=2\: \Leftrightarrow \: (x^{2}+3x-4)=0$
$(x+4)(x-1)=0\: \Rightarrow \: x=-4\: atau\: x=1$ Kedua: $x-3=0\: \Rightarrow \: x=3\: :\left\{\begin{matrix} x=3 &, 3^{2}+3(3)-2=16 &positif \\ x=2& (konstan) & positif \end{matrix}\right.$
memnuhi
Ketiga: $x-3=1\: \Rightarrow \: x=4$
Keempat: $x-3=-1\: \Rightarrow \: x=2\left\{\begin{matrix} x=2 &,2^{2}+3(2)-2=8 &genap \\ x=2 & (konstan) &genap \end{matrix}\right.$
Ternyata juga memenuhi.
Jadi Solusi dari persamaan di atas adalah: $-4,\: 1,\:2,\: 3,\: 4$ .
6. Tentukan nilai $x$ bila $x^{x^{4}}=4$ .
Jawab :
Perhatikan bahwa $x^{x^{4}}=4$ . Pangkatkan 4 masing-masing ruas, sehingga
$\left ( x^{x^{4}} \right )^{4}=\left ( 4 \right )^{4}\\\\ maka\\\\ \left ( x^{4} \right )^{x^{4}}=\left ( 4 \right )^{4}\\\\ \Rightarrow \: \: x^{4}=4\\\\ diperoleh\: \: \sqrt[4]{x^{4}}=\sqrt[4]{4}\\\\ \left | x \right |=\sqrt[4]{2^{2}}\: \Leftrightarrow \: \left | x \right |=\sqrt{2}\\\\ jadi,\\\\ x=\sqrt{2}\: \: atau\: \: x=-\sqrt{2}$ .
7. Carilah nilai $x$ jika $x^{-x}=4$ .
Jawab :
$x^{-x}=2^{2}\: \Rightarrow \: x^{-x}=\left ( -2 \right )^{2}\\\\ sehingga\\\\ x^{-x}=\left ( -2 \right )^{-\left ( -2 \right )}\\\\ Jadi,\\\\ x=-2$ .
B. Fungsi Logaritma
1. Fungsi logaritma dengan $a>1$
Perhatikan ilustrasi berikut

[Sumber]

2. Fungsi logaritma dengan $0<a<1$
Perhatikan pula ilustrasi berikut

[Sumber]

Sifat-sifat operasi pada logaritma

[Sumber]

Silahkan anda pelajari beberapa bentuk persamaan logaritma dan langkah penyelesaiannya.

$\LARGE\fbox{Contoh Soal}$

1. Tentukan nilai x yang memenuhi persamaan:

$^{2}\log (x^{2}-7x+12)=1$

Jawab:

ingat bahwa untuk $^{a}\log b=c\: \: \Leftrightarrow \: \: b=a^{c}$

Sehingga

$x^{2}-7x+12=2^{1}$

$x^{2}-7x+10=0$

$(x-2)(x-5)=0$

Jadi, $x=2\: \: atau\: \: x=5$

2. Tentukan penyelesaian dari $\log (x+3)=\log (x^{2}-9)$

Jawab:

$x+3=x^{2}-9\: \Rightarrow \: x^{2}-x-12=0$

$(x+3)(x-4)=0\: \Leftrightarrow \: x=-3\: \: atau\: \: x=4\: \left\{\begin{matrix} x=-3 &,tidak\: \: memenuhi \\ x=4&,memenuhi \end{matrix}\right.$

Catatan: lihat syarat numerus.

3. Carilah jumlah akar-akar dari persamaan

$^{2}\log ^{2}x+7^{2}\log x+12=0$

Jawab:

$misalkan \: \: p=^{2}\log x\: \: \: maka\: \: \: ^{2}\log ^{2}x=\left ( ^{2}\log x \right )^{2}=p^{2}$

Sehingga

$p^{2}+7p+12=0\: \: \Rightarrow \: \: (p+4)(p+3)=0$ .

Maka untuk

$p+4=0\: \: \Leftrightarrow \: \: ^{2}\log x+4=0\: \: \Leftrightarrow \: \: ^{2}\log x=-4$

didapatkan nilai $x=2^{-4}=\frac{1}{16}$

untuk

$p+3=0\: \: \Leftrightarrow \: \: ^{2}\log x+3=0\: \: \Leftrightarrow \: \: ^{2}\log x=-3$

didapatkan nilai $x=2^{-3}=\frac{1}{8}$

Jadi, jumlah akar-akar yang dimaksud adalah $\frac{1}{8}+\frac{1}{16}=\frac{3}{16}$

4. Tentukan nilai x + y dari sistem persamaan

$\begin{matrix} ^{7}\log x &+ &^{7}\log y &=&5 \\ ^{7}\log x^{3}&- &^{7}\log y^{4} &=&1 \end{matrix}$

Jawab:

Misalkan

$^{7}\log x=a\: \: \: dan\: \: \: ^{7}\log y=b$

maka

$\begin{matrix} a &+ & b &= &5 \\ 3a& - & 4b & = &1 \end{matrix}$

dengan eliminasi ataupun substitusi diperoleh $\left\{\begin{matrix} a=3 \\ b=2 \end{matrix}\right.$

untuk $a=3\: \: \Rightarrow \: \: ^{7}\log x=3\: \: x=7^{3}=343$
untuk $b=2\: \: \Rightarrow \: \: ^{7}\log y=2\: \: y=7^{2}=49$

Jadi, nilai x + y = 343 + 49 = 392

$\LARGE\fbox{Latihan Soal}$

Carilah solusi dari persamaan eksponen $(7x-1)^{3x-2}=(x-5)^{3x-2}$
Carilah solusi untuk $9\times \sqrt{(\frac{1}{27})^{2x-1}}=\sqrt{243}$
Gambarlah grafik fungsi $f(x)=3^{x+1}$ , untuk $x\epsilon \left \{ -3,-2,-1,0,1,2,3,4 \right \}$
Carilah solusi untuk $(x^{2}-9x+19)^{3x+4}=(x^{2}-9x+19)^{4x+2}$
Gambarlah grafik fungsi $f(x)=^{2}\log (x+1)$ , untuk $x\epsilon \left \{ -3,-2,-1,0,1,2,3,4 \right \}$
Carilah nilai $x$ jika $2^{x+1}+2^{x+2}+2^{x+3}=56$ .

C. Aplikasi Fungsi Eksponensial dan Fungsi Logaritma

1. Fungsi Eksponensial

a. Pertumbuhan(growth)

Misalkan seseorang menabung di sebuah bank menggunakan sistem bunga majmuk dengan bungan p% pertahun, maka jumlah uangnya selah $n$ adalah $M_{n}$ adalah

$\LARGE\boxed{M_{n}=M\left ( 1+\frac{p}{100} \right )^{n}}$

b. Peluruhan(decay)

Misalkan suatu zat radioaktif yang meluruh dapat kita nyatakan dengan

$\LARGE\boxed{x\left ( t \right )=x\left ( 0 \right ).e^{-\lambda .t}}$

dengan

$x\left ( t \right )$ = massa yang tersisa setelah t detik
$x\left ( 0 \right )$ = massa awal
$\lambda$ = konstanta peluruhan

2. Fungsi Logaritma
Misalkan suatu senyawa kimiawi dihitung nilai pH

$\LARGE\boxed{pH=-\log \left [ H^{+} \right ]}$

dengan

$pH$ adalah sifat keasaman
$\left [ H^{+} \right ]$ adalah konsentrasi ion hidrogen dalam mol per liter pada suatu larutan

Misalkan juga dalam bidang fisika berkaitan dengan taraf intensitas bunyi (TI). Dimana TI adalah perbandingan antara intensitas bunyi dengan intensitas ambang

$\LARGE\boxed{TI=10\log \frac{I}{I_{0}}}$

$\LARGE\fbox{Contoh Soal}$ 1. Ahmad menyimpan uangnya di bank sebesar Rp200.000,00 dengan tingkat suku bunga majmuk 10% pertahun. Tentukan lamanya waktu supaya uang simpanan Ahmad di bank menjadi Rp600.000,00
Jawab:
Diketahui $\left\{\begin{matrix} M_{n} &= & Rp 600.000,00 \\ M &= & Rp200.000,00 \\ p & = &10 \end{matrix}\right.$ .
$M_{n}=M.\left ( 1+\frac{p}{100} \right )^{n}$ ,
$600.000=200.000.\left ( 1+0,10 \right )^{n}$ ,
$\left ( 1,1 \right )^{n}=\frac{600000}{200000}=3$ ,
$n\log \left ( 1,1 \right )=\log 3$ ,
$n=\frac{\log 3}{\log \left ( 1,1 \right )}$ ,
$t=\frac{0,4771}{0,0414}$ , (gunakan kalkulator)
$t=11,53$ .
Jadi, waktu yang dibutuhkan adalah 11, 53 tahun
2. Massa suatu zat radioaktif dirumuskan yang meluruh dapat dinyatakan dengan rumus
$x\left ( t \right )=x\left ( 0 \right ).e^{-\lambda .t}$
a. Jika $x(t)=7,1,\: x(0)=10,5,\: dan\: \lambda =1,3\times 10^{-3}$ , maka tentukan $t$ dalam tahun
b. Jika $t_{\frac{1}{2}}$ adalah waktu yang dibutuhkan sehinggga massa yang tertinggal sama dengan setengah dari jumlah massa awal, tunjukkan bahwa $t_{\frac{1}{2}}=\frac{0,693}{\lambda }$
Jawab:
diketahui $x\left ( t \right )=x\left ( 0 \right ).e^{-\lambda .t}$ .
$\log x(t)=\log x(0).e^{-\lambda .t}$ ,
$\log x(t)=\log x(0)-\lambda .t\log e$ ,
$\lambda .t\log e=\log x(0)-\log x(t)$ ,
$t=\frac{\log x(0)-\log x(t)}{\lambda \log e}$ ,
$t=\frac{\log 10,5-\log 7,1}{1,3\times 10^{-3}.\log 2,71828}=300,8 \: \: tahun$
b. diketahui bahwa $\left\{\begin{matrix} t & = & t_{\frac{1}{2}} \\ x(t) & = & \frac{1}{2}x(0) \end{matrix}\right.$
sehingga
$\frac{1}{2}x(0)=x(0).e^{-\lambda .t_{\frac{1}{2}}}$ ,
$e^{-\lambda .t_{\frac{1}{2}}}=\frac{1}{2}$ ,
$e^{\lambda .t_{\frac{1}{2}}}=2$ ,
$\lambda. t_{\frac{1}{2}}\log e=\log 2$ ,
$t_{\frac{1}{2}}=\frac{\log 2}{\lambda . \log e}$ ,
$t_{\frac{1}{2}}=\frac{0,3010}{\lambda .(0,434)}$ ,
$t_{\frac{1}{2}}=\frac{0,693}{\lambda }$ .
terbukti
3. Jika diketahui konsentrasi ion hidrogen dari jus jeruk adalah $6,32\times 10^{-4}$ , maka tentukan $pH$ dari jus jeruk tersebut!
Jawab:
$pH=-\log \left [ H^{+} \right ]$ ,
$pH=-\log \left ( 6,32\times 10^{-4} \right )$ ,
$pH=-\left ( \log 6,32+\log 10^{-4} \right )$ ,
$pH=-\log 6,32+4$ ,
$pH=-0,8007+4=3,1993$ .
Jadi, $pH\approx 3,2$ .

4. Misalkan sebuah komputer saat kondisi baru bernilai $N_{0}$ rupiah.. Andaikan komputer tersebut setelah $t$ tahun mengalami penyusutan sebesar $N_{0}\left ( \frac{2}{3} \right )^{t}$ . Harga komputer tersebut akan bernilai sebesar $\frac{N_{0}}{9}$ setelah …. tahun.
Jawab:
diketahui harga awalnya $N_{0}$ rupiah. Dan setelah $t$ tahun , maka harganya akan menjadi $N_{t}$ . Jika $N_{t}=\frac{N_{0}}{9}$ , maka
$N_{0}-N_{0}\left ( \frac{2}{3} \right )^{t}=\frac{N_{0}}{9}$ ,
$1-\left ( \frac{2}{3} \right )^{t}=\frac{1}{9}$ ,
$\left ( \frac{2}{3} \right )^{t}=\frac{8}{9}$ , masing-masing ruas di-logkan, sehingga
$\log \left ( \frac{2}{3} \right )^{t}=\log\frac{8}{9}$ ,
$t=\frac{\log \frac{8}{9}}{\log \frac{2}{3}}=\frac{\log 8-\log 9}{\log 2-\log 3}=\frac{3\log 2-2\log 3}{\log 2-\log 3}$ .

$\LARGE\fbox{Latihan Soal}$

Populasi hewan langka berkurang 20% setiap tahunnya. Jika sekarang populasinya tinggal 10.000 ekor, dalam berapa tahun tersebut tinggal 1000 ekor saja (gunakan rumus $y=y_{0}.e^{kt}$ , serta anggap bahwa pelestarian hewan tersebut tidak membuahkan hasil)
Dalam sebuah laboratorium sedang diteliti tentang pertumbuhan bakteri. Jika mula-mula terdapat 25 bakteri dan setelah 2 jam jumlah bakteri menjadi 100, maka berapakah jumlah bakteri setelah 4 jam (asumsikan bakteri terus bertambah dan dirumuskan dengan $k(x)=k.a^{x}$
perhatikan gambar di atas yang menunjukkan grafik fungsi tekanan udara terhadap perubahan ketinggian

a) Tunjukkan bahwa P sebagai fungsi h yang paling mendekati adalah $P(h)=C.2^{ah},\: \: \: dengan\: \: C>0\: \: dan\: \: a<0$
b) Jika $P(h)=A.f(h)$ , tunjukkan bahwa $P(10)=1013.\frac{f(10)}{f(0)}$ .

Sumber Referensi

Luji, Willa Adrian Sukoco. 2006. Matematika Bilingual untuk SMA Kelas XII IPA Semester 1 & 2. Bandung: Yrama Widya.
Sukino. 2013. Matematika Kelompok Peminatan Matematika dan Ilmu Alam untuk SMA/MA Kelas X. Jakarta: Erlangga.
Tampomas, Husein. 1999. Seribu Pena MatematikaSMU Kelas 2. Jakarta: Erlangga.
Tung, Khoe Yao. 2012. Pintar Matematika SMA Kelas XII IPA Untuk Olimpiade dan Pengayaan Pelajaran. Yogyakarta: ANDI.
Wirodikromo, Sartono. 1996. Matematika untuk SMU Jilid 6 Kelas 2. Jakarta: Erlangga.
_________, Algebra: Teoria con 8000 Problemas Propuestos y Resueltos.

Punya Radit

Hari ini kamu aneh

Kenapa dit?

Hari ini kamu lebih cantik dari biasanya..

Rabu, 31 Oktober 2018

FAKTA-FAKTA LOUIS TOMLINSON! NO.7 MENCENGANGKAN

Cara Mudah Menggam

bar Struktur Lewis Suatu Molekul

MATEMATIKA WAJIB? BAWA SUSAH AJA

Materi Persamaan dan Pertidaksamaan Linier Kelas 10

Logaritma Lewat Ajaaaa~~~~

Fungsi Eksponen dan Logaritma

Untuk Kamu

Jadwal Sholat

Self Healing

Labels

Blog Archive

Berita

Kategori Materi

Rabu, 31 Oktober 2018

Cara Mudah Menggam bar Struktur Lewis Suatu Molekul

Materi Persamaan dan Pertidaksamaan Linier Kelas 10

Untuk Kamu

Jadwal Sholat

Self Healing

Labels

Blog Archive

Berita

Kategori Materi

Cara Mudah Menggam

bar Struktur Lewis Suatu Molekul